Notiuni introductive

 1. Notiuni de baza

1.1. Spatii metrice

Multimea X se numeste spatiu metric daca pentru orice pereche de elemente x, y din X s-a definit o functie reala d(x,y) numita distanta de la x la y sau metrica în X, cu urmatoarele proprietati:

a) d(x,y)³ 0;

b) d(x,y) = 0, daca si numai daca x = y;

c) d(x,y) = d(y,x);

d) d(x,y) £ d(x,z) + d(z,y).

Penultima relatie exprima proprietatea de simetrie a functiei distanta, iar ultima exprima inegalitatea triunghiului. Un spatiu metric se va nota prin (X,d), daca în multimea X s-a introdus metrica d.

În X se pot introduce metrici diferite d₁, d₂, … , d_n si de aceea spatiile metrice (X,d₁), (X,d₂), … vor fi considerate distincte. Elementele lui X se numesc puncte.

Exemple:

1. Dreapta reala R este multimea tuturor numerelor reale. Distanta dintre doua puncte x si y apartine lui R si se defineste prin functia:

.

2. Planul euclidian R² se obtine considerând multimea tuturor perechilor de numere reale x(x ₁ ,x ₂ ), y(h ₁ ,h ₂ ) etc. si metrica euclidiana definita prin:

.

1.2. Spatiu liniar

 Fie K o multime de numere reale (complexe). Multimea X se numeste spatiu liniar real (complex) daca în aceasta multime sunt definite operatia de adunare si operatia de înmultire a elementelor multimii X cu elementele multimii K, adica pentru orice x, y Î X si a, b Î K avem:

a x + b y Î X

Se cer sa fie îndeplinite urmatoarele conditii:

a) " x, y Î X: x+y = y+x;

b) " x, y, z Î X: (x+y)+z = x+(y+z);

c) " x Î X: x+q =x;

d) " x, y, z Î X: x+y =z are solutie unica;

e) " x, y Î X," a Î K: a (x+y) =a x+a y;

f) " x Î X," a, b Î K: (a +b )x = a x+b x;

g) " x Î X: 0 * x = q;

Elementele spatiului liniar se numesc puncte sau vectori.

Exemple:

1. Spatiul vectorial real m-dimensional R^m. Elementele spatiului R^m sunt vectori coloana de forma:

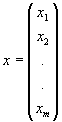; unde x₁, x₂, … , x_m Î R sunt coordonatele vectorului x.

Pentru comoditate folosim x^T = ( x₁ , … , x_m ).

Spatiul R^m este un spatiu liniar real.

2. Fie C_m([a,b]) o multime de functii continue definite pe intervalul [a,b] cu valori în R^m. Pentru f, g Î C_m([a,b]) si a Î R întelegem:

(f+g)(t) = f(t) + g(t); t Î [a,b]

(a f)(t) = a f(t).

Deci C_m([a,b]) este spatiu liniar.

1.3. Spatiu normat

 Presupunem ca în spatiul liniar X exista o functie determinata cu valori reale, notata cu astfel încât " x Î X

R¹,

: X® R.

Daca pentru orice x, y Î X si a Î K:

;

;

;

, atunci functia

o numim norma, iar spatiul X se numeste spatiu normat.

Orice spatiu vectorial normat este un spatiu metric (X, d) daca se defineste distanta d data prin:

Prin sfera închisa (deschisa) de raza r într-un spatiu normat X întelegem multimea punctelor x ale acestui spatiu care satisfac inegalitatea:

,

unde x₀ este centrul sferei, iar numarul real r este raza ei.

Notatie: B(x₀ , r) = {xÎ X / , r ³ 0 }.

Sirul elementelor spatiului X, x_n Î X este convergent în norma catre elementul x Î X, daca:

, când n® ¥.

Elementul x îl numim limita sirului x_n.

Exemple:

1. În spatiul R^m se pot defini câteva norme diferite. Normele cele mai frecvent folosite în acest spatiu sunt:

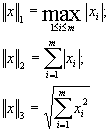
Aceste norme sunt echivalente.

 2. În spatiul C_m([a,b]) putem lua ca norma:

Convergenta în norma definita astfel se numeste convergenta uniforma.

 1.4. Spatiu Banach – Spatii Hilbert

 Fie x_n un sir de elemente ale unui spatiu liniar normat X.

Sirul x_n este sir Cauchy daca pentru orice e >0 exista un numar natural n₀ Î N astfel încât pentru orice n, m > n₀ avem:

.

Un spatiu normat X se numeste spatiu complet daca orice sir Cauchy al elementelor din X are o limita în acest spatiu.

Spatiul Banach este un spasiu liniar, normat si complet.

Presupunem ca în spatiul liniar X exista o functie de doua variabile cu valori complexe    <×, × >: X * X ® C;valoarea acestei functii pentru argumentele x si y cu x, y Î X o vom nota cu x^Ty, unde T nu este operatia de transpunere, ci un simbol.

Daca x^Ty îndeplineste conditiile:

a) " x, y Î X: x^Ty = y^Tx;

b) " x₁, x₂, y Î X; " a, b Î C: (a x₁ + b x₂)^Ty=a (x₁^Ty) + b (x₂^Ty);

c) " x Î X: x^Tx ³ 0; x^Tx =0 Þ x=0,

atunci functia respectiva se numeste produs scalar si se noteaza cu <x,y>.

Obs.:

, deci spatiul X este un spatiu normat.

Spatiul complet în care este generat produsul scalar se numeste spatiu Hilbert.

Consecinta:

Spatiu Hilbert este un spatiu Banach în care norma este generata de un anumit produs scalar.

Importanta practica a spatiilor Hilbert deriva din posibilitatea definirii notiunii de ortogonalitate.

Prin definitie, doua elemente x, y Î R sunt ortogonale si se noteaza prin x^ y daca este satisfacuta conditia:

<x,y>=0.

Exemple de spatii Hilbert

1. În spatiul R^m, produsul scalar poate fi:

, unde x^T = [x₁,x₂,…,x_m],

y = [y₁,y₂,…,y_m].

2. În spatiul C_m([a,b]) produsul scalar poate fi:

.

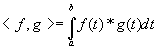1.5. Spatiul L^p

 Fie T un spatiu de masura. Daca p ³ 1, vom spune ca aplicatia x : T ® este de putere p integrabila daca:

1. x este masurabila

2. este integrabila

Teoreme:

1. Spatiul L^p este un spatiu vectorial real.

Dem:

Într-adevar, daca x Î L^p si a Î R, atunci a x este masurabila.

Pe de alta parte,

În al doilea rând, fie x Î L^p, y Î L^p. Avem

.

Dar                                    , deci x+y Î L^p.

2. Spatiul L^p este un spatiu Banach.

Dem:

Consideram un sir de elemente pozitive din L^p, astfel încât . Punem .

Vom arata ca x Î L^p.

Punem                 . Pe baza inegalitatii lui Minkowski avem:

.

Dar, y ® x, deci:

si x Î L^p.

1.6. Operator liniar

 Fie doua multimi oarecare X si Y. Daca este determinata legea dupa care unui element oarecare x Î X i se asociaza un singur element y Î Y spunem ca a fost definita o functie de la multimea X la multimea Y.

Functiile le vom nota cu f, g, h, …

Notatie: f : X ® Y, f(x) = y, unde y este valoarea functiei f în punctul x.

Functiile se mai definesc cu ajutorul legilor, ca de exemplu când X = Y = R¹, x Î X, o asociere de forma:

este o functie f : R¹ ® R¹.

Contraexemplu: x = y², x Î X si y Î Y cu X = Y = R¹ nu determina nici o functie f : X ® Y.

Fie B₁ si B₂ doua spatii Banach. Spunem ca functia A : B₁ ® B₂ este un operator liniar si continuu (marginit ), daca:

a) A(a x+b y)=a A(x)+b A(y) " x, y Î B₁, " a, b Î K;

b) exista o constanta L astfel încât pentru orice x Î B₁ avem:

.

Exemplu:

Fie B₁, B₂ doua spatii Banach si A un operator liniar A : B₁ ® B₂. Daca exista o functie A^-1 : B₂ ® B₁ astfel încât:

A^-1A = E₁

AA^-1 = E₂, unde E_I operator identitate pentru B_I, i = 1, 2, atunci A^-1 se va numi operator invers al lui A. A^-1 este un operator liniar.

(A₁+A₂)(x) = A₁(x) +A₂(x), " x Î B₁

(a A)(x) = a A(x) , " x Î B₁, " a Î R.

Multimea de operatori liniari este un spatiu liniar pe care îl vom nota cu L(B₁,B₂). Pe acest spatiu, L(B₁,B₂) se poate determina norma:

, " x Î B₁, de unde rezulta urmatoarea inegalitate:

, pentru orice A si x.

Spatiul L(B₁,B₂) este un spatiu Banach.

1.7. Derivata, diferentiala

 Fie B₁ , B₂ doua spatii Banach, iar f o functie f : B₁ ® B₂.

Daca pentru un punct x al spatiului B₁ si pentru oricare element h Î B₁, cu proprietatea: , exista relatia:

f(x+h) – f(x) = A(x) * h + w(x,h),

unde: A(x) este un operator liniar în raport cu h depinzând de x si daca:

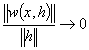, când , spunem ca functia f este diferentiabila în punctul x.

Operatorul A(x) care depinde de x si este liniar si continuu în raport cu h este derivata în sens Frechet a functiei f în punctul x, iar valoarea operatorului A(x) în punctul h, notat cu A(x)h, se numeste diferentiala functiei f în punctul x pentru o crestere h.

Derivata functiei f într-un punct x o notam cu:

sau .

La operarea derivatelor Frechet trebuie acordata o atentie deosebita caror spatii le apartin valorile functiilor.

Daca, de exemplu, f : B₁ ® B₂, atunci:

f¢ : B₁ ® L(B₁ , B₂),

f² : B₁ ® L(B₁ ,L(B₁ , B₂)).

În consecinta pentru x Î B₁, h₁ Î B₁, h₂ Î B₂ avem:

f² : B₁ ® L(B₁ , B₂),

f² (x)h₁: B₁ ® B₂,

f² (x)h₁h₂ = (f² (x)h₁)(h₂) Î B₂.

1.8. Teorema mediei

 Fie B un spatiu Banach si fie x Î B, y Î B, x ¹ y. Numim interval închis cu extremitatile x si y o multime de puncte de forma:

p(t) = x + t(y - x); 0 £ t £ 1.

Notatie: [x , y].

Multimea punctelor p(t), 0 < t < 1 se va numi interval deschis si se va nota (x,y)

 Teorema

Fie B₁ si B₂ doua spatii Banach si fie f : B₁ ® B₂. Presupunem ca functia f are o derivata continua. În acest caz pentru x₁, x₂ Î B₁ avem:

.

 Corolar

Fie f o functie diferentiabila în B₁, iar x₀ un punct din B₁ (x₀ Î B₁). În acest caz pentru orice x₁, x₂ Î B₁ avem:

.

1.9. Erori

 1. Surse de erori

Solutiile obtinute prin metode numerice sunt aproximative erorilor.

Sursele de erori pot fi:

a) gradul de adecvare al modelului matematic. Daca modelul matematic este mai fin erorile se pot diminua.

b) erori initiale sau erori în datele de intrare. Erorile initiale se formeaza din erori de masurare datorate impreciziei instructiunii de masurat. Erorile de observatie sunt neregulate sau întâmplatoare.

c) Erori de metoda. Apar prin folosirea unei metode numerice.

d) Erori de calcul care sunt de trunchiere sau de rotunjire.

Eroarea de trunchiere se obtine de exemplu prin calcului unei serii înlocuindu-l printr-o suma partiala. Eroarea de rotunjire se obtine astfel: daca pe ultima zecimala a unui numar real avem cifrele 0, 1, 2, 3, 4, atunci denumim prin lipsa daca ultima cifra se lasa la o parte si penultima cifra zecimala se lasa neschimbata; astfel denumim prin adaos, când ultima cifra zecimala lasata la o parte este 5, …, 9 si penultima cifra se mareste cu o unitate.

2. Studiul erorilor sau propagarea erorilor

Fie aÎ R valoare exacta sau ideala a unei marimi. În practica în locul valorii exacte se lucreaza cu valoare aproximata . Considerând în locul lui a pe se comite o eroare care trebuie masurata.

Vom nota cu eroarea care se comite si se foloseste denumirea de eroare absolutã.

Valoarea 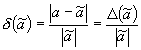se numeste eroare relativa.

Se poate întâmpla ca în alte lucrari eroarea relativa sa fie definita prin formula:

Numarul  se numeste o limita pentru eroarea absoluta daca:

.

Numarul se numeste o limita pentru eroarea relativa daca:

.

Daca este o limita pentru eroarea absoluta, atunci este o delimitare pentru eroarea relativa.

1.10. Polinoame ortogonale

 Fie [a,b] Ì R si w : [a,b] ® R o functie continua, pozitiva pe (a,b) si astfel încât:

,

numita functie pondere.

Se noteaza prin multimea functiilor f : [a,b] ® R , continue pe [a,b] si care satisfac conditia:

.

este un spatiu liniar fata de operatiile obisnuite de adunare si înmultire cu un scalar a functiilor, iar

defineste un produs scalar pe                              .

O multime de functii F Ì  este ortogonala pe intervalul [a,b] în raport cu functia pondere w daca pentru orice f, g Î F , f ¹ g.

F se numeste ortonormala daca în plus pentru toti f Î F.

 Exemplu:

Polinoamele lui Legendre

Fie a = -1, b=1 si w(t) = 1.

Avem

, unde U_I este solutia ecuatiei diferentiale

.

Prin urmare, U_I este un polinom de gradul 2 având pe –1 si 1 radacini multiple de ordinul i, adica , C fiind o constanta care poate fi determinata din conditia de ortonormare.

Polinomul l_i definit prin:

se numeste polinomul lui Legendre de gradul I, iar

polinomul lui Legendre cu coeficientul lui tⁱ egal cu 1.

Avem formula de recurenta:

cu si .

Folosind aceasta formula de recurenta se deduc în mod succesiv expresiile polinoamelor , k=2, 3, …:

Astfel:

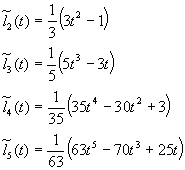
1.11. Teoremele de scufundare ale lui Sobolev

Teorema1 ( inegalitatea lui Sobolev )

Fie x(s) o functie continuu diferentiabila în domeniul convex D si            . (1)

Atunci este valabila inegalitatea:

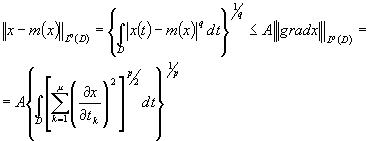
unde: -

este valoarea medie a functiei x în domeniul D

-mesD este masura Lebesgue a multimii D

-A este o constanta.

Observatie

Daca p=2 si m ³ 2, inegalitatea se scrie sub forma:

.

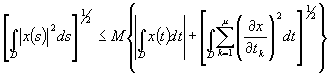Introducem câteva spatii functionale, ale caror elemente vor fi functiile continuu diferentiabile în domeniul D.

Consideram spatiul . Punem:

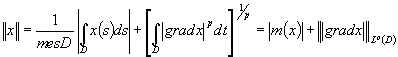
Daca este considerat ca functie din L^q(D), inegalitatea lui Sobolev are urmatoarea forma:

Operatorul de scufundare, adica operatorul care asociaza elementului aceeasi functie este operator liniar continuu.

Teorema (Sobolev-Kondrasev)

În conditia relatiei (1) operatorul de scufundare, care asociaza unei functii din aceeasi functie considerata ca element din L^q(D), este compact.

Teorema

În conditia m <p, operatorul de scufundare, considerat ca operator din în C(D), este continuu si compact.

Mai consideram un spatiu în care norma se definestecu ajutorul derivatelor superioare, si anume spatiul tuturor functiilor de l ori continuu diferentiabile în domeniul D, notat cu , în care norma se defineste astfel:

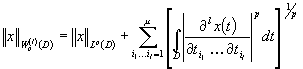
Teorema

În conditiile operatorul de scufundare a spatiului ( D domeniu

convex) în spatiul L^q(D¢ ) ( D¢ suprafata n -dimensionala în D ) este compact. În plus, la deformarea continua a suprafetei D¢ în functie de un parametru, acest operator depinde continuu de parametru.

Aplicatie

Se considera problema la frontiera

Cautam solutiile printre functiile care au integrala Dirichlet finita:

,

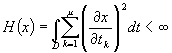adica vom considera . Rezulta ca xÎ L²(S). Dimensiunea n a varietatii S este egala cu m -1 si

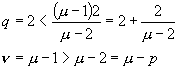
În plus,

, adica valorile functiei x pe suprafata de frontiera reprezinta limita (în medie ) a valorilor ei din interior.

Astfel, o functie cu integrala Dirichlet finita trebuie sa aiba valori la frontiera de patrat integrabil pe suprafata.

1.2.Teoria generala a metodelor iterative în cazul ecuatiilor si sistemelor neliniare

1.2.1.Metode iterative în cazul ecuatiilor neliniare

 Fie f : [a,b] ® R si fie ecuatia f(x) = 0 , x Î [a,b].

Aceasta ecuatie se transforma sub forma iterativa j (x) = x, unde: j : [a,b] ® R si x Î [a,b].

Transformarea asupra ecuatiei trebuie facuta în asa fel încât solutia x* a ecuatiei f(x) = 0 sa fie solutie si pentru ecuatia iterativa si invers.

f(x* ) = 0 Û j (x* ) = x*, x* Î [a,b].

Solutia ecuatiei j (x) = 0 se numeste punct fix pentru functia j.

Functia iterativa j genereaza un sir iterativ {x_k}_{kÎ N} astfel:

x₀ = a;

x₁ = j (x₀);

…………

x_k+1 = j (x_k)

…………

Acest sir va converge catre x* care este solutia ecuatiei initiale.

Presupunem ca ecuatia admite o unica solutie x* în [a,b].

 Teorema lui Banach

Fie ( X, r ) un spatiu metric complet. Fie j : X ® X o contractie, adica exista a Î [0,1) astfel încât: r ( j (x) , j (y) ) £ a r ( x , y ), " x, y Î X.

Atunci functia j va admite un unic punct fix care se poate obtine ca limita sirului iterativ {x_k}_{kÎ N} dat de x_k+1 = j (x_k) pentru un punct x₀ Î X arbitrar.

 Teorema

Daca j este derivabila pe I = [x₀ - d , x₀ + d ], d > 0 si derivata j ¢ satisface inegalitatea 0 £ ½ j ¢ (x)½ £ m < 1, " x Î I si punctul x₁ = j (x₀) satisface inegalitatea ½ x₁ – x₀ ½ £ (1 – m) * d, atunci putem forma sirul iterativ {x_k}_{kÎ N} astfel încât x_kÎ N, " kÎ N.

Exista limita sirului x_k: si x* este singura radacina a ecuatiei j (x) = x în I.

 Dem:

Se aplica teorema de punct fix a lui Banach. Se alege X = I.

Trebuie sa verificam ca j ne duce din I în I, adica j : I ® I.

Trebuie sa demonstram ca pentru orice " x Î I Þ j (x) Î I.

Calculam:

½ j (x) - x_0½ = ½ j (x) - j (x₀) + j (x₀) - x_{0½ £ ½ j} (x) - j (x₀)½ +½ j (x₀) -x_0½ = (*) si conform teoremei lui Lagrange avem:

(*) = ½ j ¢ (x ) * (x-x₀)½ + ½ x₁ - x_0½ £ m½ x - x_0½ +½ x₁ - x_0½ £ m * d +(1 – m ) * d = =m * d + d - m * d = d.

Deoarece j este o contractie avem:

½ j (x) - j (y) ½ = ½ j ¢ (x )(x - y)½ £ m*(x - y) " x, y Î I , x Î (x,y); unde a = m.

În continuare aplicam aceasta teorema pentru câteva metode iterative alegând în mod convenabil functia iterativa j.

1) f(x) = 0 ½ + x

Adunând ecuatia cu x formam ecuatia iterativa f(x) + x =x , unde j (x) = f(x) + x, rezultând ca j (x) = x.

Daca f este derivabila pe I = [x₀ - d ,x₀ + d ], d > 0 si ½ 1 + f¢ (x) ½ £ m < 1 pe I si ½ f(x₀)½ £ (1 – m)*d, atunci putem forma sirul {x_k}_{kÎ N} cu regula iterativa x_k+1 = j (x_k) , astfel încât x_k Î I, " kÎ N; exista limita sirului lim x_k = x* si x* este singura solutie a ecuatiei j (x) = x.

2) f(x) = 0 ½ * w ¹ 0

w f(x) = 0 ½ + x

Adunând ecuatia cu x formam ecuatia iterativa w f(x) + x = x, unde j (x) = w f(x) + x, rezultând ca (x) = x.

Daca f este derivabila pe I = [x₀ - d ,x₀ + d ] , d > 0 si ½ 1 + w f¢ (x) ½ £ m < 1 pe I si ½ w f(x₀)½ £ (1 – m)*d, atunci putem forma sirul {x_k}_{kÎ N} cu regula iterativa x_k+1= j (x_k), astfel încât x_k Î I, " kÎ N; exista limita sirului lim x_k = x* si x* este singura radacina în I a ecuatiei j (x) = x.

3) f(x) = 0

Împartind ecuatia cu (-f¢ (x)) si adunând rezultatul cu x obtinem ecuatia iterativa , unde              , rezultând ca j (x) = x cu f¢ (x)¹ 0

Daca f este derivabila de doua ori pe I = [x₀ - d ,x₀ + d ], d > 0 si f¢ (x) ¹ 0 pentru orice x Î I si 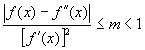pe I si ,

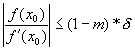atunci putem forma sirul {x_k}_{kÎ N} cu regula iterativa x_k+1= j (x_k), astfel încât x_k Î I, " kÎ N; exista limita sirului lim x_k = x* si x* este singura radacina în I a ecuatiei j (x) = x.

2.2. Metode iterative în cazul sistemelor neliniare

 Fie F : DÌ R^n® Rⁿ, D ¹ Æ cu F(x) = q _Rⁿ, unde F = (F₁,F₂,…,F_n) ; F_i : D ® R.

Sistemul initial F(x) = q _Rⁿ se pune sub forma iterativa x = j (x), unde

j : D¢ Ì Rⁿ ® Rⁿ.

Aceasta transformare trebuie facuta în asa fel încât solutia x* a primei ecuatii sa fie punct fix pentru functia j si invers.

 Teorema lui Jacobi

Fie j Î C¹(), unde Ì D¢ ( exista derivate partiale ale lui j si sunt continue ) si daca ,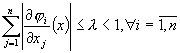

" x Î ( convexa ) si j () Ì , atunci sistemul de ecuatii neliniare x = j (x) admiteo unica solutie.

 Dem:

Se aplica teorema de punct fix al lui Banach pentru functia j.

Avem :j : ® si Ì Rⁿ este spatiu complet, deoarece orice multime închisa într-un spatiu complet este completa.

Aratam ca j este o contractie.

Se alege norma vectoriala ¥, . Aplicam teorema de medie a lui Lagrange:

.

Trecând la modul obtinem:

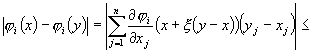
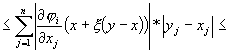
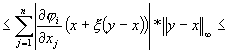
Fie x, y fixati si , atunci obtinem:

.